Sadržaj objave
Što su logičke izjave?
Riječ logika dolazi od grčke riječi logos što znači riječ, razum, razlog, misao, zakon.
Logička izjava je tvrdnja koja može biti istinita (True) ili lažna (False).
Kao i kod bitova, ako je u logičkoj izjavi tvrdnja istinita, možemo je označiti jedinicom – 1 (True), a ako je lažna nulom – 0 (False). Umjesto punog naziva True možemo skraćeno pisati T, a umjesto False F.
Znamo da računalo sve podatke prepoznaje kao nizove bitova – jedinica i nula pri čemu jedan bit uvijek ima jedno od dva moguća stanja (jedan ili nula).
Povezivanjem bitova nastaju složeniji podaci. Za povezivanje bitova u nizove složenijih podataka koristimo se logičkim izjavama i elektroničkim sklopovima zasnovnim na njima.
Primjeri logičke izjave
| Izjava | Objašnjenje | Opis |
| 10 + 5 = 15 | Ova tvrdnja je istinita. | 1 Istina (True) |
| “Nakon noći slijedi dan” | Ova tvrdnja je istinita. | 1 Istina (True) |
| “U Varaždinu svaki dan pada kiša” | Ova tvrdnja nije istinita. | 0 Laž (False) |
| “Varaždin je središte Varaždinske županije “ | Ova tvrdnja je istinita. | 1 Istina (True) |
| 9 < 5 | Ova tvrdnja nije istinita. | 0 Laž (False) |
| 3 = 3 | Ova tvrdnja je istinita. | 1 Istina (True) |
| “A < B” | Ova tvrdnja je istinita. | 1 Istina (True) |
| “Ponedjeljak > Utorak” | Ova tvrdnja nije istinita. | 0 Laž (False) |
Subjektivne izjave
Tvrdnju “ona je jako zaljubljena u njega” ne možemo smatrati logičkom tvrdnjom stoga što je tvrdnja subjektivna i ne možemo se provjeriti.
U njoj je sadržano puno više od dva odgovora (istinitog ili lažnog): možda je jako zaljubljena, možda je malo zaljubljena, možda nije zaljubljena, itd.
Odnosi između logičkih izjava
Znakove <, >, =, <=,=>, != koje smo dosad rabili za usporedbu brojeva možemo upotrijebiti i za uspostavljanje odnosa u logičkim izjavama između dana u tjednu ili slova hrvatske abecede.
| Znak | Značenje |
| < | “je manje od” , “prethodi”, “dolazi ispred” |
| > | “je veće od”, “slijedi”, “dolazi iza” |
| = | “je jednako”, “je istodobno” |
| <= | “je manje ili jednako”, “dolazi prije ili istodobno” |
| => | “je veće ili jednako”, “dolazi iza ili istodobno” |
| != | “je različito” ,”nije jednako” |
Pojmovi
Logička izjava – je tvrdnja koja može biti istinita ili lažna.
Istinitost logičke izjave – prikazujemo binarnim stanjem 1.
Lažnost logičke izjave – prikazujemo binarnim stanjem 0.
Logička varijabla
Logičku izjavu Zagreb je glavni grad Republike Hrvatske možemo zamijeniti simbolom npr. A te možemo pisati:
A = Zagreb je glavni grad Republike Hrvatske.
Simbol A predstavlja u ovom primjeru potpunu logičku izjavu. Kad simbol predstavlja logičku izjavu nazivamo ga varijablom.
Zaključimo: Logička varijabla je zamjena za neku logičku izjavu (tj. njezina skraćenica).
| Prema tome umjesto: | možemo pisati: |
| logička izjava B = “četvrtak < petak” je istinita, | B = 1 |
| logička izjava C = “100 > 50” je istinita i | C = 1 |
| logička izjava M = “srijeda > četvrtak”. | M = 0 |
Jednostavne logičke funkcije
Na logičkim varijablama mogu se izvoditi razne operacije. Na taj način nastaju logičke funkcije.
Logičke izjave međusobno se kombiniraju u logičke izraze.
Prisjetimo se zadatka:
◦Ako pada kiša, nosim kišobran.
◦Ovdje imamo povezane logičke izjave. Radnja u drugoj izjavi će se odvijati ovisno o istinitosti prve izjave.
◦Primijenimo u ovom zadatku logičke varijable.
◦ Prvu logičku izjavu (“Ako pada kiša“) označimo sa A.
◦Drugu logičku tvrdnju (“nosim kišobran“) označimo sa B.
◦Logički izraz: “Ako pada kiša, nosim kišobran.” možemo napisati u obliku funkcije: B = A ili f(B) = A
| Ako pada kiša | nosim kišobran |
| 1 Istina (T) | 1 Istina (T) |
| 0 Nije istina (F) | 0 Nije istina (F) |
Strujni krug
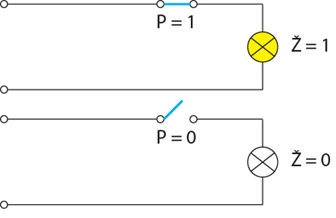
Primjere logičkih izjava možemo uočiti promatranjem strujnog kruga, kako stanje žarulja ovisi o stanjima prekidača.
◦Mi možemo oblikovati logičku izjavu “prekidač je uključen” koja je istinita kada vodič do žarulje nije prekinut i koja je lažna kada je vodič prekinut. Označimo tu izjavu slovom P. Ako je P = 1 onda je Ž = 1.
◦Možemo izreći i drugu logičku izjavu “žarulja svijetli”. Ta će izjava biti istinita onda kada žarulja svijetli, a lažna kada žarulja ne svijetli. Označimo tu izjavu slovom Ž. Ako je P = 0 onda je Ž = 0.
Tablica istinitosti
Zaključak o tome u kakvom je stanju žarulja u ovisnosti o prekidaču iz prethodnoga primjera možemo opisati i tablicom istinitosti.
| Prekidač | Žarulja |
| 1 | 1 |
| 0 | 0 |
Složene logičke funkcije
Logičke funkcije mogu se izraditi i s dvjema ili više logičkih izjava.
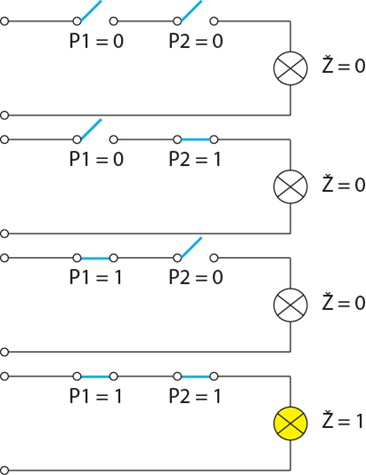
Iz slike vidljivo je da će dovod struje biti prekinut kada je bilo koji prekidač otvoren.
To ćemo izreći pomoću sljedećih logičkih izjava:
- logička izjava P1: “prekidač P1 je uključen”,
- logička izjava P2: “prekidač P2 je uključen”.
Promatrajući sliku možemo zaključiti sljedeće:
- ako je P1 = 0 i P2 = 0 onda je Ž = 0;
- ako je P1 = 0 i P2 = 1 onda je Ž = 0;
- ako je P1 = 1 i P2 = 0 onda je Ž = 0;
- ako je P1 = 1 i P2 = 1 onda je Ž = 1.
Pojmovi
Logičke varijable – je zamjena za neku logičku izjavu.
Vrijednosti logičkih varijabli – može biti istinita (True) ili lažna (False).
Vrijednosti bita – Istinitost logičke varijable (True) iskazujemo stanjem bita (1), a ne istinost (laž) logičke varijable (False) stanjem (0).
Zadaci za učenike
Literatura: Moj portal 3.0 Školska knjiga